5.13.2 Kaplan-Meier
This is the simplest and perhaps the most common type of survival analysis. The standard result of such an analysis is Kaplan-Meier curves, which typically show a staircase-shaped curve that goes downward along the x-axis (time). The curve itself shows the survival rate as a function of time and is given by the following formula:
In addition to graphs, key figures for the current analysis population
are also displayed. Kaplan-Meier can also be used to create bivariate
analysis of survival rates, where differences between groups of the
population are examined. This is done through the use of a by-option where separate curves can be displayed for each group in the same graph.
Kaplan-Meier is a non-parametric analysis form for simple survival analysis, but can also be used as a tool to set up more advanced analyses, such as multivariate Cox analysis: By studying Kaplan-Meier curves, one can compare survival rates for the different groups of individuals grouped through explanatory variables and see if there are significant differences in survival rates between, for example, women and men. If the curves do not overlap, this is a sign that the current explanatory variable is good to use as an explanatory variable for a multivariate analysis.
After you have your data set ready for survival analysis, cf. section 5.11.1, you can run a Kaplan-Meier analysis by using the
kaplan-meier command where you first specify the variable "event"
and then "time" (the order is important).
Examples:
Typical outputs:
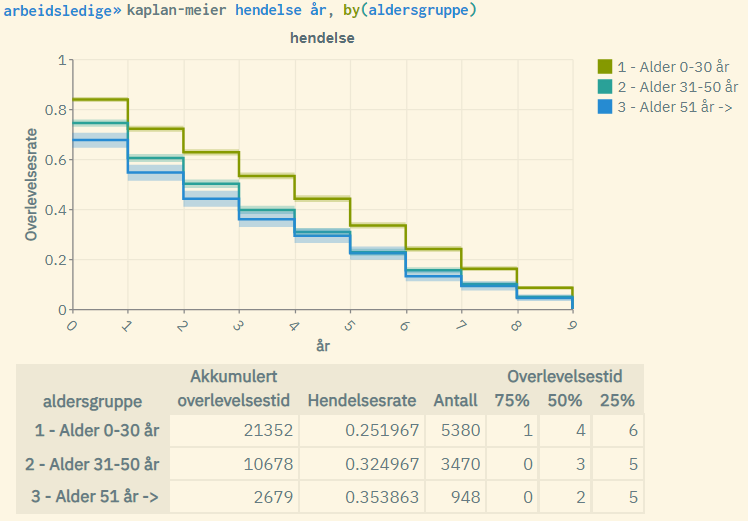
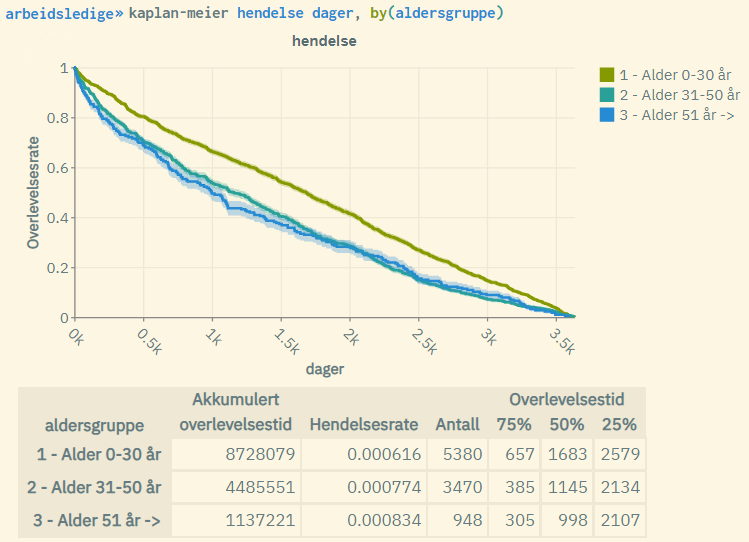
-
The curves are given by the Kaplan-Meier formula for each age group. The youngest age group performs the best with a higher "survival rate" (are less likely to become unemployed over time).
-
The shaded areas represent the standard log-log 5% confidence interval associated with the survival rate for each age group. These will be less visible in larger populations.
-
"Akkumulert overlevelsestid": Cumulative survival time, often referred to as "time at risk". This is the sum of time measured over all units in the population (within each age group).
-
"Hendelsesrate": Event rate. This is the number of events occurred (number of units with event = 1) divided by cumulative survival time.
-
"Antall": Population size, i.e. the number of units (for each age group).
-
"75%": Time measured where survival rate = 0.75 (for each age group).
-
"50%": Time measured where survival rate = 0.5 (for each age group). Also known as "median survival time".
-
"25%": Time measured where survival rate = 0.25 (for each age group).
Example: How to prepare data for survival analysis, amongst others Kaplan-Meier analyses